تعریف سیستم و انواع آن

ضمن عرض سلام خدمت شما همراهان همیشگی، در آموزش های قبلی از درس سیگنال ها و سیستم ها با سیگنال های زوج و فرد آشنا شدید. در این آموزش قصد داریم که شما را با تعریف سیستم و انواع آن را برای شما توضیح دهیم. تا آخر این مقاله با ما همراه باشید.

فهرست مطالب این مقاله

یک سیستم از نظر ریاضی به عنوان یک تبدیل کننده یا تابع تعریف می گردد، در واقع این سیستم سیگنال ورودی که می توانیم آن را x(t) نامگذاری کنیم را به عنوان ورودی دریافت می کند و در آخر سیگنال y(t) که آن را خروجی می نامیم به ما تحویل می دهد. اگر بخواهیم سیستم را در ریاضیات تعریف کنیم، می توانیم بگوئیم که سیگنال خروجی در هر لحظه، تابعی از مقادیر سیگنال ورودی در همه زمان ها و همچنین تابعی از خود زمان می باشد. این مطلب را می توانیم به صورت زیر نمایش دهیم.

در رابطه بالا نماد $T\left \{ \right \}$ بیانگر عملگر سیستم است که بر روی وردی اثر می کند و خروجی را تولید می کند. اگر بخواهیم رابطه بالا را توصیف کنیم می توانیم بگوئیم که خروجی در هر لحظه دلخواه $t_{0}$ ، تابعی از ورودی در همه زمان ها یا $\small -\infty <t<+\infty$ و تابعی از خود $t_{0}$ می باشد. اگر بخواهیم این موضوع را بهتر بیان کنیم می توانیم بگوئیم که برای به دست آوردن خروجی در حالت کلی باید مقدار ورودی در همه زمان ها و حتی خود زمان $t_{0}$ مشخص باشد. به تعریفی که در بالا بیان شد تعریف لحظه ای سیستم می گوئیم، زیرا به ما می گوید که در هر لحظه خروجی سیستم چگونه بدست می آید.

اتصال سیستم ها

تقریباً تمامی سیستم ها را می توانیم به شیوه های مختلفی به یکدیگر متصل کرد، در این جا ما به سه نوع از اتصال سیستم ها یعنی اتصال سری، اتصال موازی و اتصال فیدبک اشاره خواهیم کرد.

اتصال سری (متوالی)

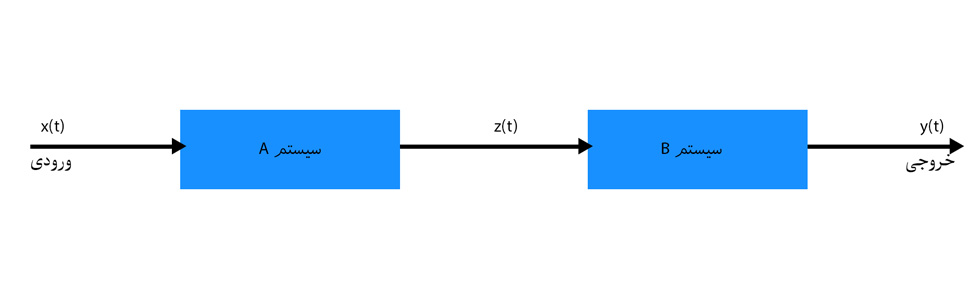
در این نوع اتصال ورودی و خروجی سیستم A به ترتیب x(t) و z(t) خواهند بود. همچنین ورودی و خروجی سیستم B به ترتیب z(t) و y(t) هستند. در واقع در اتصال سری هر آنچه از سیستم A خارج می شود به عنوان ورودی به سیستم B داده می شود. ورودی و خروجی کلی سیستم x(t) و y(t) هستند.

اتصال موازی

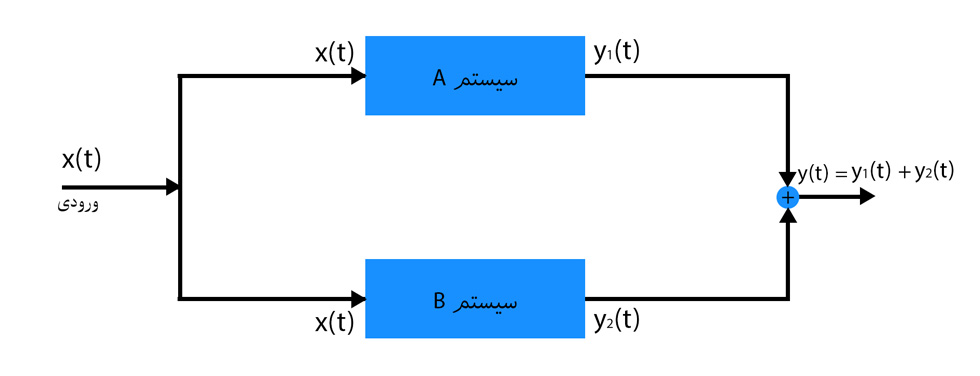
در اتصال موازی هر دو سیستم ورودی های یکسانی را دریافت می کنند، ولی خروجی بسته به عملکرد هر کدام از سیستم ها متفاوت خواهد بود. در اتصال موازی که در تصویر بالا مشاهده می کنید ورودی و خروجی سیستم A به ترتیب x(t) و $\small y_{1}(t)$ هستند. از طرف دیگر ورودی و خروجی سیستم B به ترتیب x(t) و $\small y_{2}(t)$ هستند. خروجی کلی سیستم مجموع خروجی دو سیستم A و B یعنی $\small y(t) = y_{1}(t) + y_{2}(t)$ خواهند بود.

اتصال فیدبک

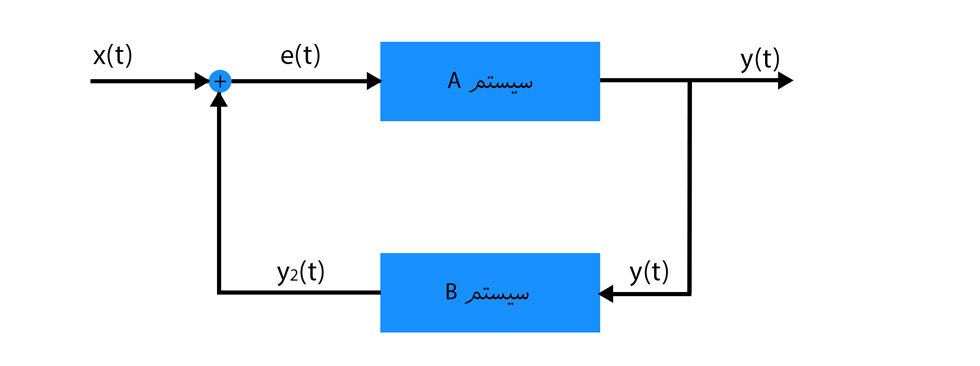
اتصال سیستم ها به صورت فیدبک حالت های مختلفی دارد، ما به عنوان مثال اتصال بالا که معمولاً در تمامی کتاب ها مشاهده می کنید را برای شما آورده ایم. در این نوع اتصال ورودی و خروجی سیستم A به ترتیب $\small e(t) = x(t) + y_{2}(t)$ و y(t) هستند و خروجی سیستم B به ترتیب y(t) و $\small y_{2}(t)$ هستند. ورودی و خروجی کلی سیستم با اتصال فیدبک به ترتیب x(t) و y(t) هستند. با اتصال فیدبک به وفور در درس کنترل خطی سر و کار خواهید داشت.

آشنایی با خواص سیستم ها

در ادامه مقاله تعریف سیستم و انواع آن، حال قصد داریم که شما را با خواص سیستم های مختلف آشنا کنیم. سیستم ها بر اساس ورودی آن ها که زمان پیوسته باشد یا زمان گسسته، به دو دسته سیستم های زمان پیوسته و زمان گسسته تقسیم می شوند. همچنین می توان بر اساس ارتباط ورودی و خروجی یک سیستم نیز آن ها را دسته بندی کرد، به عنوان مثال دسته ای از سیستم ها رابطه بین ورودی و خروجی آن ها به صورت خطی است که به آن ها سیستم های خطی می گویند. در ادامه با انواع خواص سیستم ها نظیر : خطی بودن، بدون حافظه بودن، علّی بودن، تغییر ناپذیری با زمان، پایداری و وارون پذیری آشنا خواهیم شد.

سیستم های خطی

در ادامه مقاله تعریف سیستم و انواع آن حال به سراغ سیستم های خطی می آییم و شروط خطی بودن یک سیستم را بررسی می کنیم. به سیستم هایی خطی می گوئیم که رابطه بین ورودی و خروجی آن ها به صورت خطی باشد یا به عبارت بهتر دو خاصیت همگنی و خاصیت جمع پذیری که در ادامه آن ها را توضیح خواهیم داد در آن ها توأماً برقرار باشند.

خاصیت همگنی

به سیستم هایی همگن می گوئیم که اگر در آن ها ورودی را k برابر کنیم، خروجی آن ها نیز k برابر خواهد شد. به عنوان مثال اگر ورودی یک سیستم x(t) و خروجی آن y(t) باشد، آنگاه اگر ورودی را k برابر یعنی kx(t) آنگاه خروجی آن هم k برابر یعنی ky(t) خواهد شد. در حالت کلی k یک ثابت مختلط است و حتی می تواند مقدار صفر هم باشد.

در واقع سیستمی که چنین خاصیتی دارد، در پاسخ به ورودی k برابر، خروجی k برابر را تولید خواهد کرد.

خاصیت جمع پذیری

در سیستم هایی که خاصیت جمع پذیری در آن ها برقرار است، پاسخ به جمع ورودی ها برابر جمع خروجی ها خواهد شد. به عنوان مثال اگر پاسخ به ورودی $\small x_{1}(t)$ برابر با $\small y_{1}(t)$ و پاسخ به ورودی $\small x_{2}(t)$ برابر با $\small y_{2}(t)$ باشد، آنگاه پاسخ به ورودی $\small x_{1}(t) + x_{2}(t)$ برابر $\small y_{1}(t) + y_{2}(t)$ خواهد شد.

تساوی بالا بیان می کند که پاسخ به مجموع ورودی ها برابر با مجموع خروجی ها خواهد بود. برای اثبات خطی بودن یک سیستم کافی است که هر دو خواص همگنی و جمع پذیری در آن توأماً برقرار باشند، آنگاه به آن سیستم یک سیستم خطی می گوئیم. اگر در یک سیستم خطی پاسخ به ورودی $\small x_{1}(t)$ برابر با $\small y_{1}(t)$ و پاسخ به ورودی $\small x_{2}(t)$ برابر با $\small y_{2}(t)$ باشد، آنگاه پاسخ به ورودی $\small \alpha x_{1}(t) + \beta x_{2}(t)$ برابر با $\small \alpha y_{1}(t) + \beta y_{2}(t)$ می شود.

$\large T\left \{ \alpha x_{1}(t) + \beta x_{2}(t) \right \} = \alpha T\left \{ x_{1}(t) \right \} + \beta T\left \{ x_{2}(t) \right \}$

سیستم های بدون حافظه (لحظه ای)

سیستم بدون حافظه را سیستمی می گویند که خروجی آن در هر لحظه دلخواه $\small t_{0}$ ، به مقادیر ورودی و خروجی لحظات قبل و یا بعد $\small t_{0}$ بستگی نداشته باشد. به عنوان مثال سیستم y(t) = x(-t) یک سیستم حافظه دار است به این دلیل که خروجی در لحظه t = 2 به ورودی در لحظه t = -2 وابسته است. یا به عنوان مثالی دیگر سیستم y(t) = cos(x(t)) را در نظر بگیرید، در این سیستم برای محاسبه خروجی در لحظه t باید به ورودی در همان لحظه t نگاه کنیم و سپس از آن کسینوس بگیریم تا خروجی را بدست آوریم. در واقع خروجی در لحظه t در این سیستم، به لحظات قبل و بعد از آن وابسته نیست، پس این سیستم یک سیستم بدون حافظه یا لحظه ای است.

سیستم های علّی (بدون پیش بینی)

به سیستمی علّی می گویند که خروجی آن در لحظه دلخواه $\small t_{0}$ ، به مقادیر ورودی در لحظات بعد از $\small t_{0}$ بستگی نداشته باشد. به عنوان مثال سیستم $\small y(t) = x(\frac{t}{2})$ را در نظر بگیرید، اگر خروجی در لحظه t = -2 را در این سیستم بخواهیم، این خروجی به مقدار ورودی در لحظه t = -1 وابسته است. پس این سیستم یک سیستم غیرعلّی می باشد.

سیستم های TI (سیستم های تغییر ناپذیر با زمان)

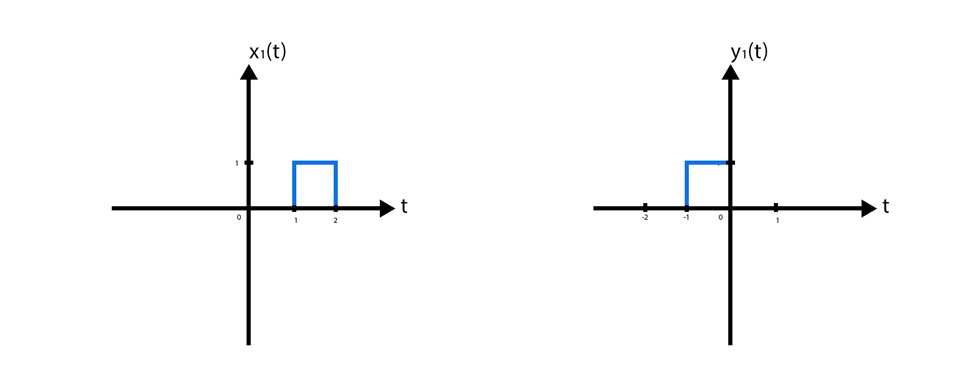
به سیستمی تغییر ناپذیر با زمان می گویند که رفتار و مشخصات آن با گذشت زمان تغییر نکنند، یا به عبارت بهتر رابطه بین ورودی و خروجی آن مستقل از زمان باشد و تغییر نکند. اگر سیستمی TI نباشد، آنگاه به آن TV (تغییر پذیر با زمان) می گوئیم. به عنوان مثال سیستم y(t) = x(t+2) را در نظر بگیرید. این سیستم ورودی را گرفته و آن را به مقدار 2 واحد به سمت چپ انتقال می دهد. به تصاویر زیر توجه کنید.

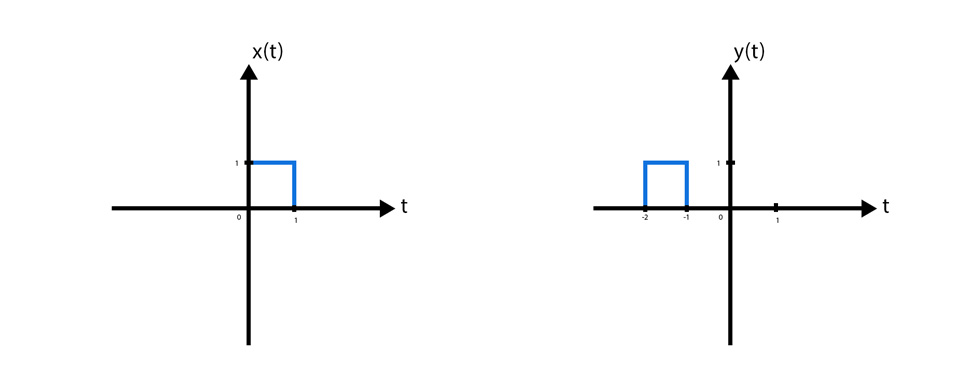
حال اگر در این سیستم، ورودی را به مقدار 1 = $\small t_{0}$ واحد به سمت راست انتقال دهیم، خروجی نیز دقیقاً به همان مقدار واحد به سمت راست انتقال پیدا خواهد کرد. زیرا این سیستم دوباره ورودی را می گیرد، و 2 واحد به سمت چپ منتقل می کند. یعنی پاسخ سیستم به ورودی $\small x_{1}(t) = x(t-1)$ برابر با $\small y_{1}(t) = y(t-1)$ خواهد شد. پس سیستم y(t) = x(t+2) یک سیستم تغییر ناپذیر با زمان است.

سیستم های پایدار

به سیستمی یک سیستم پایدار می گویند که به ازای تمام ورودی های کراندار یا محدود، خروجی کراندار یا محدود بدهد.

سیستمی اگر حداقل به ازای یک ورودی کراندار، خروجی بیکران بدهد، یک سیستم ناپایدار است. در واقع برای بررسی پایداری یک سیستم، ابتدا فرض می کنیم که یک ورودی کران دار به سیستم داده شده است، اگر به ازای این ورودی خروجی نیز کراندار شود، آنگاه پایداری سیستم قطعی و می توانیم بگوئیم که سیستم پایدار است. به عنوان مثال سیستم $\small y(t) = x^{2}(t)$ را در نظر بگیرید، اگر ورودی سیستم یعنی x(t) محدود باشد، آنگاه خروجی سیستم یعنی $\small y(t) = x^{2}(t)$ نیز محدود خواهد بود و می توانیم بگوئیم که این سیستم پایدار است.

سیستم های وارون پذیر (معکوس پذیر)

به سیستمی سیستم وارون پذیر می گوئیم، که به ازای ورودی های متمایز، خروجی های متمایز بدهد. در واقع سیستمی وارون پذیر است که به ازای دو ورودی متفاوت خروجی یکسانی را نتیجه ندهد. به عبارت بهتر در سیستم های وارون پذیر، می توان ورودی را از روی خروجی بدست آورد، به این دلیل که هر خروجی دقیقاً متناظر با یک ورودی است. در واقع سیستم های وارون پذیر را می توان شبیه توابع یک به یک در نظر گرفت.

برای سیستم هایی که وارون پذیر هستند، می توان یک یا چندین معکوس تعریف کرد به صورتی که اگر سیستم اصلی را با سیستم وارون سری کنیم، خروجی سیستم وارون همان ورودی سیستم اصلی خواهد بود.

به عنوان مثال از یک سیستم وارون پذیر، سیستم y(t) = 3x(t) را در نظر بگیرید، واضح است که این سیستم، هر ورودی به آن داده شود، را در عدد 3 ضرب کرده و به خروجی می فرستد. اگر x(t) = cost باشد، آنگاه خروجی این سیستم برابر با y(t) = 3cost خواهد بود، واضح است که این سیستم وارون پذیر است، زیرا که این سیستم به ازای هر ورودی متمایز، یک خروجی متمایز ایجاد می کند. دو شرط لازم و کافی برای بررسی وارون پذیری یک سیستم وجود دارد، که در ادامه آن ها را بررسی می کنیم.

شرط لازم : اولین شرط که شرط لازم هم می باشد برای وارون پذیر بودن یک سیستم این است که ورودی همه زمان ها و تمام مقادیر ورودی به خروجی منتقل شوند، به عبارت بهتر خروجی به ورودی در همه زمان ها و مقادیر آن وابسته است. سیستمی که این شرط لازم را نداشته باشد، نمی توان آن را یک سیستم وارون پذیر دانست. زیرا گفتیم که اگر یک سیستم وارون پذیر باشد، باید بتوان اطلاعات ورودی را از روی خروجی به دست آورد، اما سیستمی که برخی از اطلاعات ورودی را حذف کرده و به خروجی منتقل نمی کند، چنین شرایطی را نخواهد داشت و یک سیستم وارون پذیر نیست.

شرط لازم و کافی : شرط لازم و کافی برای این که بگوئیم یک سیستم وارون پذیر است یا خیر این است که بتوان ورودی سیستم یعنی x(t) را به صورت یکتا و بدون ابهام از روی خروجی یعنی y(t) بدست آوریم. اگر سیستمی دو شرط گفته شده را داشته باشد، قطعاً می توانیم بگوئیم که یک سیستم وارون پذیر است.

خلاصه مقاله تعریف سیستم و انواع آن

در این مقاله در ابتدا با تعریف سیستم آشنا شدید و سپس با انواع سیستم و خواص آن ها نظیر: خطی بودن، بدون حافظه بودن، علّی بودن، تغییر ناپذیر بودن با زمان (TI)، پایدار بودن، وارون پذیر بودن (معکوس پذیر) آشنا شدید.

امیدوارم که مقاله تعریف سیستم و انواع آن برای شما عزیزان مفید واقع شده باشد، هرگونه پرسش در مورد این مقاله را در قسمت نظرات مطرح کنید.

برچسب ها

یاسین بهره ملا آگوست 19, 2022آخرین به روز رسانی: آگوست 19, 2022

0 2,292 خواندن این مطلب 8 دقیقه زمان میبرد

دیدگاهتان را بنویسید لغو پاسخ

یاسین بهره ملا
خیلی ممنون از حسن توجه شما، ویرایش شد. موفق باشید....
یاسین بهره ملا
ممنونم از توجه شما، اصلاح شد....
Ahmadreza Mohammadi
با سلام، ممنونم از مطالب خوبتون در بدست آوردن v2 بجای مقدار...
یاسین بهره ملا
خواهش میکنم، نظر لطف شماست. موفق باشید....
محمد
ممنون مهندس بابت وب سایت خوبت🤞😊...

تعریف سیستم و انواع آن – آشنایی با خواص سیستم ها