دروس برقکنترل خطی

تابع حساسیت در سیستم های کنترل خطی – حساسیت چیست ؟

یاسین بهره ملا ارسال ایمیل ژوئن 28, 2022آخرین به روز رسانی: جولای 18, 2022
0 1,492 خواندن این مطلب 6 دقیقه زمان میبرد

در پست های قبلی با قاعده میسون (Mason) از درس سیستم های کنترل خطی آشنا شدید، در این پست قصد داریم که با مفهوم جدیدی به نام حساسیت آشنا شویم. حساسیت در واقع یک تعریف ریاضی است که برای بررسی میزان حساسیت یک سیستم نسبت به تغییر پارامترهایش تعریف می شود. در ادامه با مقاله تعریف تابع حساسیت همراه باشید تا به طور کامل با مفهوم حساسیت در کنترل خطی آشنا شوید.

تعریف تابع حساسیت در کنترل خطی

اگر P را به عنوان یک پارامتر از سیستم مورد مطالعه در نظر بگیریم، با تغییر P خروجی سیستم مورد نظر نیز تغییر خواهد کرد. برای آنکه بدانیم پارامتر P چگونه بر خروجی سیستم تاثیر می گذارد، مفهومی به نام حساسیت را تعریف می کنیم. در واقع ما در یک سیستم تغییرات خروجی ناشی از تغییر یک پارامتر را حساسیت آن سیستم نسبت به آن پارامتر تعریف می کنیم.

مفهوم ریاضی حساسیت

همانطور که بیان کردیم، حساسیت تغییرات خروجی ناشی از تغییر پارامتری مانند P از سیستم مورد مطالعه می باشد. پس اگر بخواهیم رابطه ای ریاضی برای حساسیت بیان کنیم، آن را به صورت زیر خواهیم داشت :

\dpi{150} S_{P}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial P}{P}} = \frac{\partial( lnT)}{\partial( lnP)} = \frac{\partial T}{\partial P} \times \frac{P}{T}

مقصود از \frac{\partial T}{T} و \frac{\partial P}{P} به ترتیب تغییرات نسبی T در اثر پارامتر P و تغییرات نسبی P می باشند.

مفهوم فیزیکی تابع حساسیت

اگر T را به عنوان تابع تبدیل حلقه بسته یک سیستم در نظر بگیریم، آنگاه اگر حساسیت تابع تبدیل حلقه بسته T نسبت به تغییرات P برابر یک باشد (\large S_{P}^{T} = 1)، یعنی اینکه تابع تبدیل حلقه بسته با پارامتر P نسبت مستقیم دارد. برای درک بهتر این موضوع به مثال زیر توجه کنید.

مثال : اگر تابع تبدیل حلقه بسته سیستمی را به صورت T = \frac{K}{S + 1} داشته باشیم، آنگاه حساسیت تابع تبدیل حلقه بسته را نسبت به پارامتر K محاسبه کنید. 

با توجه به فرمولی که برای حساسیت تعریف کردیم، داریم که :

\dpi{150} S_{K}^{T} = \frac{\partial T}{\partial K}*\frac{K}{T} \Rightarrow \frac{1}{S+1} * \frac{K}{\frac{K}{S+1}} \Rightarrow S_{K}^{T} = 1

همانطور که مشخص است، پارامتر K با تابع تبدیل حلقه بسته نسبت مستقیم دارد، به همین دلیل حساسیت T نسبت به K، مقدار واحد به دست آمده است.

اگر حساسیت تابع تبدیل حلقه بسته T نسبت به تغییرات پارامتر P برابر با منفی یک باشد(S_{P}^{T} = - 1)، آنگاه می توانیم بگوئیم که تابع تبدیل حلقه بسته با آن پارامتر نسبت عکس دارد. برای درک بهتر این موضوع به مثال زیر توجه کنید.

مثال : اگر تابع تبدیل حلقه بسته یک سیستم را به صورت T = \frac{1}{K(S+1)} تعریف کرده باشیم، آنگاه حساسیت این تابع تبدیل را نسبت به تغییرات پارامتر K محاسبه کنید.

\dpi{150} S_{K}^{T} = \frac{\partial T}{\partial K}*\frac{K}{T} \Rightarrow \frac{-(S+1)}{K^{2}(S+1)^{2}}*\frac{K}{\frac{1}{K(S+1)}} \Rightarrow S_{K}^{T} = -1

همانطور که می بینید، حساسیت تابع تبدیل حلقه بسته T نسبت به تغییرات پارامتر K، برابر با منفی یک می باشد، که این موضوع به معنای رابطه معکوس پارامتر K با تابع تبدیل حلقه بسته T می باشد.

اگر حساسیت تابع تبدیل حلقه بسته نسبت به تغییرات یک پارامتر برابر با صفر شود، این بدان معناست که یعنی آن پارامتر ارتباطی با تابع تبدیل حلقه بسته ندارد. برای درک این موضوع به مثال زیر توجه کنید.

مثال : اگر تابع تبدیل حلقه بسته یک سیستم به صورت T(s) = \frac{K}{S+1} باشد، آنگاه حساسیت این تابع را نسبت به پارامتر P بیابید.

به دلیل اینکه در تابع تبدیل داده شده هیچ اثری از پارامتر P نیست، پس حساسیت تابع تبدیل حلقه بسته نسبت به تغییرات این پارامتر برابر صفر خواهد بود. در ادامه این موضوع را اثبات خواهیم کرد.

\dpi{150} S_{P}^{T(s)} = \frac{\partial T}{\partial P}*\frac{P}{T} \overset{\frac{\partial T}{\partial P} = 0}{\rightarrow} \Rightarrow S_{P}^{T(s)} = 0

همانطور که مشاهده کردید به دلیل اینکه \frac{\partial T}{\partial P} = 0 شد، حساسیت تابع تبدیل حلقه بسته نسبت به تغییرات پارامتر P برابر صفر شد و این یعنی تابع تبدیل حلقه بسته ارتباطی با متغیر P ندارد.

قاعده زنجیری 

بلوک دیاگرام سیستمی را مانند شکل زیر در نظر بگیرید :

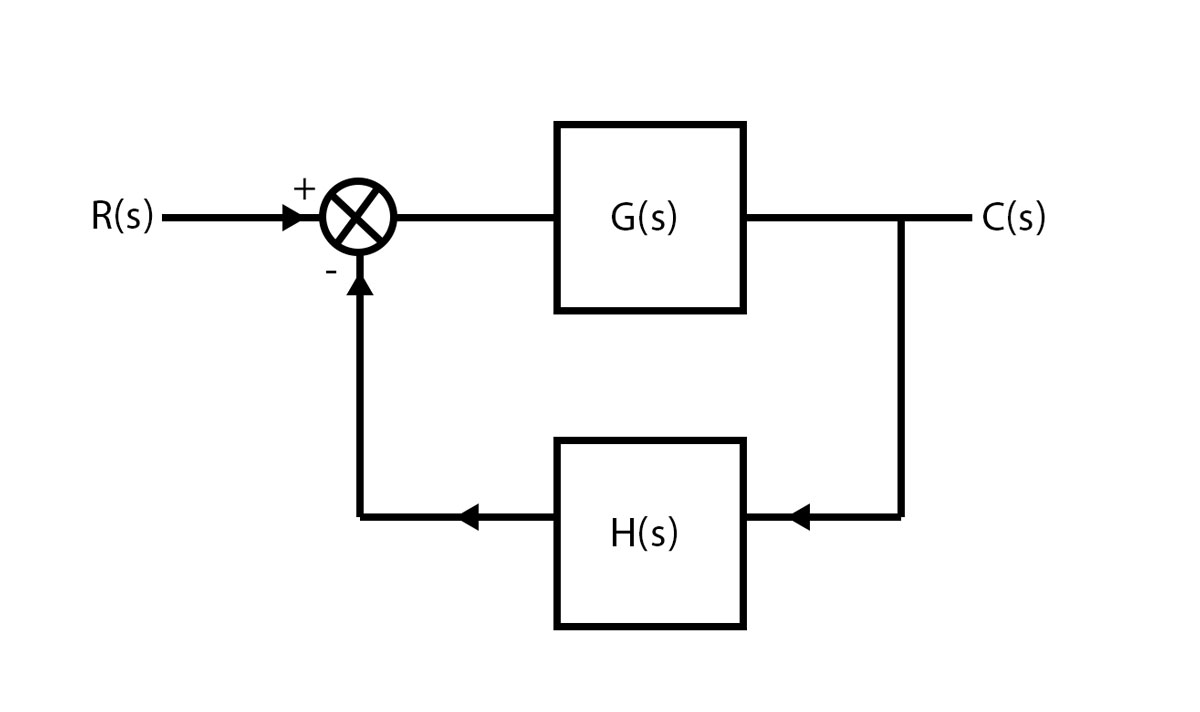
بلوک دیاگرام سیستم - کنترل خطی

فرض کنید که سیستمی با بلوک دیاگرام داده شده را در اختیار داریم و میخواهیم حساسیت تابع تبدیل حلقه بسته را نسبت به تغییرات پارامتر P موجود در این سیستم را بدست آوریم. یکی از روش هایی که می تواند فوق العاده کمک کننده و کاهش دهنده محاسبات باشد، استفاده از قاعده زنجیری می باشد. فرمول کلی قاعده زنجیری به صورت زیر بیان می شود :

\dpi{150} S_{P}^{T} = S_{G_{1}}^{T}S_{G_{2}}^{G_{1}}...S_{P}^{G_{n}}

این فرمول بیان می کند، که اگر چندین مسیر پیشرو داشته باشیم و پارامتر P در آن ها موجود باشد، می توانیم حساسیت تابع تبدیل حلقه بسته را نسبت به تغییرات پارامتر P، بدون محاسبه کامل تابع تبدیل حلقه بسته و صرفاً از طریق این فرمول به دست آوریم.

بار دیگر بلوک دیاگرام داده شده در بالا را در نظر بگیرید، فرض کنید می خواهیم حساسیت تابع تبدیل حلقه بسته T را نسبت به تغییرات پارامتر P بررسی کنیم. در این صورت می توانیم فرمول قاعده زنجیری را برای این بلوک دیاگرام به صورت زیر بیان کنیم :

\dpi{150} S_{P}^{T} = S_{P}^{T}(Feed Forward)+ S_{P}^{T}(Feed Back)

Feed Forward : مسیر پیشرو

Feed Back : مسیر فیدبک

حال سه حالت برای این فرمول را مورد بررسی قرار می دهیم :

حالت اول – اگر پارامتر P فقط در مسیر پیشرو قرار داشته باشد، یعنی اینکه پارامتر P در مسیر فیدبک (H) وجود نداشته باشد، آنگاه قاعده زنجیری را به شکل زیر به کار خواهیم برد.

\dpi{150} S_{P}^{T} = S_{G}^{T}S_{P}^{G} + 0

قسمت دوم فرمول به دلیل اینکه پارامتر P در مسیر فیدبک وجود ندارد، یا به عبارت بهتر چون که H ارتباطی با پارامتر P ندارد، این مقدار برابر با صفر شده است.

حالت دوم – اگر پارامتر P فقط در مسیر فیدبک وجود داشته باشد، یعنی اینکه پارامتر P در مسیر پیشرو (G) وجود نداشته باشد. آنگاه قاعده زنجیری را به صورت زیر به کار خواهیم برد.

\dpi{150} S_{P}^{T} = 0 + S_{H}^{T}S_{P}^{H}

قسمت اول فرمول به دلیل اینکه پارامتر P در مسیر پیشرو وجود ندارد، یا به عبارت بهتر چون که G ارتباطی با پارامتر P ندارد، این مقدار برابر با صفر شده است.

حالت سوم – اگر پارامتر P هم در مسیر پیشرو و هم در مسیر فیدبک وجود داشته باشد، آنگاه می توانیم برای محاسبه حساسیت قاعده زنجیری را به صورت زیر بیان کنیم.

\dpi{150} S_{P}^{T} = S_{G}^{T}S_{P}^{G}(feed forward) + S_{H}^{T}S_{P}^{H}(feed back)

حال که به طور کامل با مفهوم حساسیت و قاعده زنجیری آشنا شدید، با حل یک تمرین جامع به بررسی بیشتر این موضوع می پردازیم.

تمرین : حساسیت تابع تبدیل حلقه بسته را نسبت به تغییرات پارامتر P را در سیستم زیر بدست آورید.

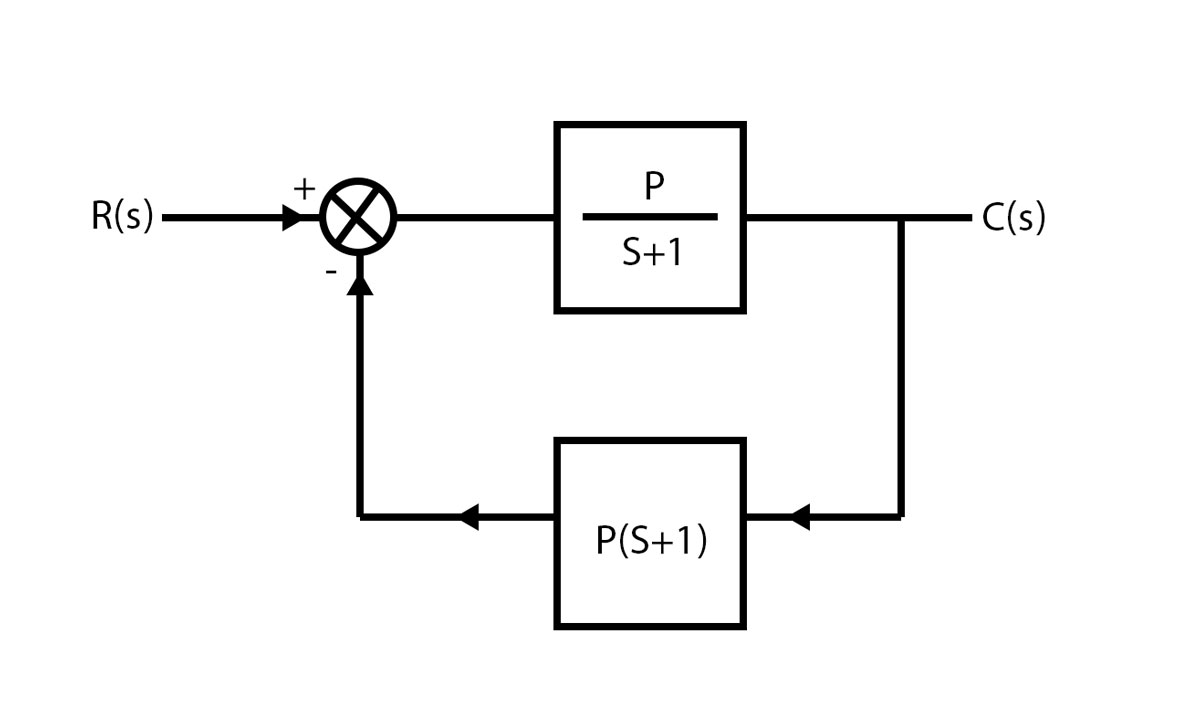
محاسبه حساسیت تابع تبدیل حلقه بسته نسبت به تغییرات پارامتر p

این سئوال را به دو روش حل خواهیم کرد، روش اول ابتدا با استفاده از قاعده زنجیری به حل این سئوال خواهیم پرداخت و سپس حل آن از طریق فرمول عمومی حساسیت را ارائه خواهیم کرد.

حل با استفاده از قاعده زنجیری :

\dpi{150} \LARGE S_{P}^{T} = S_{P}^{T} | feed forward + S_{P}^{T} feed back

همانطور که مشاهده می کنید، به دلیل اینکه متغیر P هم در مسیر پیشرو و هم مسیر فیدبک وجود دارد، فرمول قاعده زنجیری را به صورت کامل خواهیم داشت، ابتدا حساسیت تابع تبدیل حلقه بسته را نسبت به تغییرات P در مسیر پیشرو را محاسبه می کنیم، پس خواهیم داشت که :

\dpi{150} \LARGE S_{P}^{T} = S_{G}^{T} S_{P}^{G}

برای محاسبه این قسمت ابتدا باید تابع تبدیل حلقه بسته را با روش میسون که در آموزش روش میسون (Mason) با آشنا شدید، بدست آوریم. اگر G(s) = \frac{P}{s+1} و H(s) = P(s+1) در نظر بگیریم، آنگاه با استفاده از روش میسون تابع تبدیل حلقه بسته را به صورت زیر خواهیم داشت :

\LARGE T(s) = \frac{G}{1+GH} = \frac{P}{(s+1)(1+P^{2})}

حال باید حساسیت تابع تبدیل حلقه بسته را نسبت به G یعنی S_{G}^{T} را محاسبه کنیم.

\large S_{G}^{T} = \frac{\partial T}{\partial G}\frac{G}{T} \Rightarrow S_{G}^{T} = \frac{1}{(1+GH)^{2}}\frac{G}{\frac{G}{1+GH}} \Rightarrow S_{G}^{T} = \frac{1}{1+GH}

سپس حساسیت تابع تبدیل مسیر پیشرو نسبت به تغییرات پارامتر P یعنی S_{P}^{G} را محاسبه می کنیم.

\large S_{P}^{G} = \frac{\partial G}{\partial P}\frac{P}{G} \Rightarrow S_{P}^{G} = 1

حال با ضرب دو مقدار به دست آمده، حساسیت تابع تبدیل حلقه بسته نسبت به تغییرات پارامتر P در مسیر پیشرو بدست خواهد آمد.

\large S_{P}^{T} = S_{G}^{T}S_{P}^{G} = \frac{1}{1+GH}*1 \Rightarrow S_{P}^{T} = \frac{1}{1+P^{2}}

حال حساسیت تابع تبدیل حلقه بسته را نسبت به تغییرات پارامتر P در مسیر فیدبک را محاسبه می کنیم، پس خواهیم داشت:

\LARGE S_{P}^{T} = S_{H}^{T}S_{P}^{H}

ابتدا حساسیت تابع تبدیل حلقه بسته را نسبت به H یعنی S_{H}^{T} را محاسبه می کنیم.

\LARGE S_{H}^{T} = \frac{-GH}{1+GH}

حال حساسیت H نسبت به تغییرات پارامتر P یعنی S_{P}^{H} را محاسبه می کنیم.

\LARGE S_{P}^{H} = \frac{\partial H}{\partial P}\frac{P}{H} \Rightarrow S_{P}^{H} = 1

حال با ضرب دو مقدار به دست آمده، حساسیت تابع تبدیل حلقه بسته نسبت به تغییرات پارامتر P در مسیر فیدبک بدست خواهد آمد.

\LARGE S_{P}^{T} = S_{H}^{T}S_{P}^{H} = \frac{-GH}{1+GH}*1 \Rightarrow S_{P}^{T} = \frac{-P^{2}}{1+P^{2}}

در آخر اگر حساسیت تابع تبدیل حلقه بسته را نسبت به تغییرات پارامتر P هم در مسیر پیشرو و هم در مسیر فیدبک نیاز داشته باشیم، کافی است که دو مقدار به دست آمده را با یکدیگر جمع کنیم.

\dpi{150} \LARGE S_{P}^{T} = S_{P}^{T} | feed forward + S_{P}^{T} feed back

\LARGE S_{P}^{T} = \frac{1}{1+P^{2}} + \frac{-P^{2}}{1+P^{2}} = \frac{1-P^{2}}{1+P^{2}}

حل با استفاده از فرمول عمومی حساسیت :

در قسمت های قبلی تابع تبدیل حلقه بسته را بدست آوردیم، حال می خواهیم با استفاده از فرمول عمومی حساسیت، حساسیت تابع تبدیل حلقه بسته را نسبت به تغییرات پارامتر P بدست آوریم. به دلیل زیاد بودن محاسبات این روش از ذکر آن ها خودداری کردیم. البته چندتا مشتق گیری ساده هست که خودتون به راحتی می تونید اون ها را انجام بدید. 🙂

\LARGE S_{P}^{T} = \frac{\partial T}{\partial P}\frac{P}{T} \Rightarrow S_{P}^{T} = \frac{1-P^{2}}{1+P^{2}}

امیدوارم که مقاله تعریف تابع حساسیت برای شما عزیزان مفید واقع شده باشد، هرگونه سئوال در مورد این مبحث را قسمت نظرات همین مقاله مطرح کنید.

برچسب ها
یاسین بهره ملا ارسال ایمیل ژوئن 28, 2022آخرین به روز رسانی: جولای 18, 2022
0 1,492 خواندن این مطلب 6 دقیقه زمان میبرد
تصویر یاسین بهره ملا

یاسین بهره ملا

من یاسین بهره ملا، دانش آموخته رشته مهندسی برق این وب سایت رو تاسیس کردم تا آموخته های خودم و چیزهایی که میخونم رو اینجا به اشتراک بذارم تا شما بتونید به راحتی از اونا استفاده کنید. امیدوارم که خوشتون بیاد.

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد.

دکمه بازگشت به بالا