دروس برقکنترل خطی

معیار پایداری راث – هورویتز – پایداری سیستم به روش راث

یاسین بهره ملا ارسال ایمیل نوامبر 14, 2021آخرین به روز رسانی: نوامبر 15, 2021
0 3,625 خواندن این مطلب 9 دقیقه زمان میبرد

در آموزش های قبلی به شما روش میسون برای بدست آوردن تابع تبدیل بلوک های دیاگرامی را با حل چند مثال از کنکور سراسری آموزش دادیم. در این آموزش قصد داریم تا یکی از روش های بررسی پایداری سیستم های کنترل خطی یعنی معیار پایداری راث – هورویتز را آموزش دهیم. پس با این مقاله تا انتها همراه ما باشید.

معیار پایداری راث – هورویتز

معیار راث – هورویتز، روشی برای تعیین موقعیت ریشه های یک چند جمله ای با ضرایب حقیقی و ثابت است، که در آن، به منظور تعیین موقعیت ریشه های چند جمله ای، نیازی به حل و محاسبه دقیق ریشه های آن چند جمله ای نمی باشد. در واقع معیار پایداری راث یک روش جبری ساده برای تعیین پایداری سیستم های کنترل خطی می باشد.

در روش راث می توان بدون محاسبه محل دقیق ریشه های یک معادله مشخصه از یک سیستم کنترل خطی به سادگی و از روی ضرائب آن معادله مشخصه، پایداری و عدم پایداری آن سیستم را تعیین کرد. معیار پایداری راث تعداد ریشه های معادله مشخصه در نیمه راست (RHP) و نیمه چپ (LHP) صفحه S و همچنین تعداد ریشه های معادله مشخصه روی محور موهومی را نیز مشخص می کند. البته معیار راث یک سری محدودیت دارد که آن ها را بیان خواهیم کرد.

محدودیت های معیار پایداری راث

  • معیار پایداری راث در صورتی معتبر است اگر و تنها اگر معادله مشخصه، دارای ضرائب حقیقی باشد. اگر حتی یکی از ضرائب معادله مشخصه غیر حقیقی یا مختلط باشد و همچنین اگر معادله مشخصه جبری نباشد ( یعنی شامل توابعی مثل Sin و یا توابی نمائی و … باشد) در آن صورت دیگر معیار راث به سادگی قابل استفاده نخواهد بود.
  • معیار پایداری راث، فقط اطلاعاتی در مورد پایداری مطلق یک سیستم می دهد. البته به کمک روش راث می توانیم پایداری نسبی را نیز بررسی کنیم که این کار به وسیله شیفت دادن مبداء صفحه s یا دوران صفحه s امکان پذیر است ولی انجام این کار اندکی زمان بر است. همچنین معیار پایداری راث پیشنهادی را برای بهبود پایداری نسبی و یا اینکه چگونه یک سیستم ناپایدار را به یک سیستم پایدار تبدیل کنیم، ارائه نمی کند.
  • یکی دیگر از محدودیت های پایداری راث این است که این روش تنها به چند جمله ای هایی با تعداد محدود جمله قابل اعمال است و اگر چند جمله ای هایی با تعداد بی نهایت جمله داشته باشیم، نمی توانیم از معیار پایداری راث استفاده کنیم.
  • معیار پایداری راث تنها برای تعیین ریشه های معادله مشخصه نسبت به مرز پایداری jw معتبر است و این معیار را نمی توان به سایر مرزهای پایداری، مانند دایره واحد در صفحه z اعمال کرد.

مراحل تشکیل جدول در معیار پایداری راث – هورویتز

جدول راث یا آرایه راث را از روی معادله مشخصه یک سیستم یا \dpi{150} \Delta (S) آن سیستم تشکیل می دهیم. مراحل تشکیل جدول راث را به ترتیب بیان خواهیم کرد.

1 – ابتدا باید معادله مشخصه سیستم حلقه بسته یعنی \dpi{150} \Delta (S) را بدست آوریم:

a_{0}s^{6} + a_{1}s^{5} + a_{2}s^{4} + a_{3}s^{3} + a_{4}s^{2} + a_{5}s^{1} + a_{6} = 0

توجه داشته باشید که در معادله مشخصه حلقه بسته بالا، حتماً باید شرط \dpi{120} a_{6} \neq 0 برقرار باشد، برقراری این شرط به معنی این است که ریشه های معادله مشخصه که برابر با صفر هستند، باید از معادله مشخصه خارج شده باشند.

2 – تشکیل جدول راث – هورویتز :

آموزش تشکیل جدول راث - هورویتز

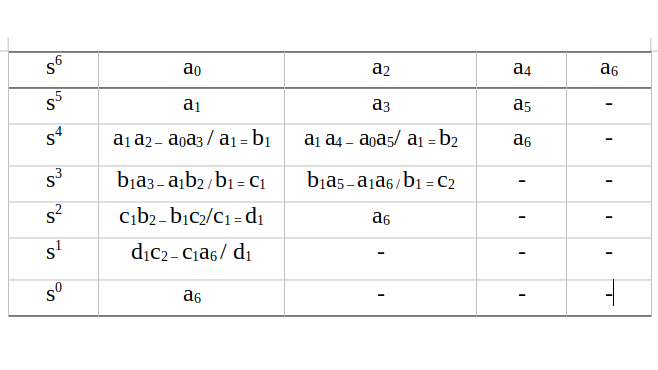
فرمول کامل تشکیل جدول معیار پایداری راث – هورویتز در جدول بالا آورده شده است و با نگاه به آن می توانید جدول راث  را برای هر معادله مشصخه ای تشکیل دهید. در تشکیل جدول راث، دو سطر اول مستقیماً از روی ضرائب معادله مشخصه نوشته می شوند و عناصر سطرهای بعدی از روی عناصر دو سطر ماقبل آن به دست می آیند. به فرمول نوشته شده در ستون های جدول بالا توجه کنید.

در فرآیند تشکیل جدول راث – هورویتز باید این نکته را در نظر داشته باشید که می توانید جملات یک سطر را در یک عدد مثبت ضرب و یا بر یک عدد مثبت تقسیم کنید. توجه داشته باشید که مجاز نیستیم که جملات یک سطر را در یک عدد منفی ضرب کنیم. بعد از تشکیل جدول راث – هورویتز برای تشخیص این که سیستم داده شده ‍ پایدار است یا خیر باید شرط زیر برقرار باشد:

شرط لازم و کافی برای پایداری سیستم، هم علامت بودن تمام عناصر ستون اول آرایه راث می باشد و تعداد تغییر علامت های ستون اول آرایه راث برابر با تعداد ریشه های ناپایدار معادله مشخصه است.

نکته : در پایداری راث لزومی ندارد که حتماً مقادیر جملات در ستون اول جدول راث را بدانیم، همین که علامت جملات ستون اول جدول راث را بدانیم می توانیم در مورد پایداری و ناپایداری سیستم داده شده قضاوت کنیم.

قواعد اولیه جدول راث :

۱ – تعداد تغییر علامت های ستون اول جدول راث برابر است با تعداد ریشه های ناپایدار(ریشه های موجود در RHP) معادله مشخصه

۲ – کلیه درایه های یک سطر از آرایه راث را می توانیم در یک عدد مثبت ضرب یا بر آن تقسیم کنیم.

۳ – تعداد درایه های هر سطر در آرایه راث برابر است با \dpi{120} \left [ \frac{n}{2} + 1 \right ]

مثال ۱ : آرایه راث برای معادله مشخصه زیر تشکیل داده و پایداری آن را بررسی کنید. 

\dpi{120} \Delta (s) = 5s^{5} + 4s^{4} + 3s^{3} + 2s^{2} + s + 1 = 0

با توجه به قواعد گفته شده برای تشکیل جدول راث، جدول راث معادله مشخصه بالا به صورت زیر تشکیل می شود:

در تشکیل جدول راث هر جا که لازم بوده است تمامی جملات یک سطر را در عددی خاص ضرب کرده ایم تا عملیات تشکیل جدول راث راحت تر صورت گیرد. با بررسی ستون اول جدول راث مشخص می شود که دو تغییر علامت رخ داده است، پس این معادله مشخصه دو ریشه در سمت راست محور jw دارد یا به عبارت بهتر دو ریشه ناپایدار دارد.

مثال ۲ : آرایه راث را برای معادله مشخصه زیر تشکیل دهید و پایداری آن را بررسی کنید.

\dpi{120} \Delta (s) = 6s^{5} + 5s^{4} + 4s^{3} + 3s^{2} + 2s + 1 = 0

آرایه راث متناظر با این معادله مشخصه به صورت زیر خواهد بود:

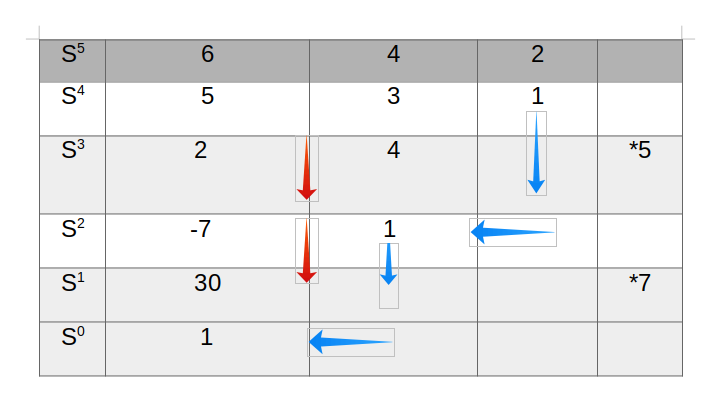
مثال حل شده از معیار پایداری راث هورویتز

با بررسی ستون اولیه آرایه راث، دو تغییر علامت در آن مشاهده خواهیم کرد که این تغییر علامت ها با فلش قرمز در جدول مشخص شده اند، چون که دو تغییر علامت در ستون اول آرایه راث رخ داده است، پس دو ریشه در سمت راست محور jw داریم، یا به عبارت بهتر این معادله مشخصه دو ریشه ناپایدار دارد.

حالات خاص در تشکیل آرایه راث 

هنگامی که آرایه راث را تشکیل می دهیم ممکن است که دو حالت ویژه برای آرایه راث رخ دهد، که در این حالت دیگر بررسی پایداری جدول راث به این آسانی نخواهد بود. در این قسمت میخواهیم این دو حالت را به طور کامل مورد بحث و بررسی قرار دهیم.

حالت ۱ : تمام عناصر یک سطر از آرایه راث صفر هستند، یا به عبارت دیگر یک سطر تماماً صفر رخ خواهد داد.

حالت ۲ : اولین درایه سطری از آرایه راث صفر و سایر درایه های آن سطر مخالف صفر هستند.

سطر تمام صفر در آرایه راث هورویتز 

سطر تمام صفر در حالتی رخ می دهد که معادله مشخصه ریشه هایی متقارن نسبت به مبدا داشته باشد، به عبارت بهتر معادله مشخصه دست کم یکی از موارد زیر را داشته باشد:

  • معادله مشخصه دارای یک یا چند ریشه موهومی داشته باشد. \dpi{120} (s=\pm j\beta )
  • معادله مشخصه یک یا چند جفت ریشه حقیقی مساوی و با علامت مخالف داشته باشد. \dpi{120} (s = \pm \alpha )
  • معادله مشخصه یک یا چند جفت ریشه مزدوج مختلط دارد که نسبت به مبدا صفحه مختلط s متقارن هستند. \dpi{120} (s=\pm \alpha \pm j\beta )

در حالت خاصی که تمام ضرایب یک سطر صفر باشند، می توانیم با مشتق گیری از معادله کمکی، ضرایب سطر تماماً صفر را بدست آوریم. جدول راث زیر را در نظر بگیرید:

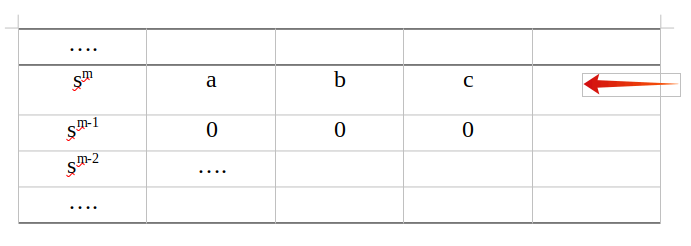
سطر تمام صفر در آرایه راث هورویتز

همانطور که در سطر \dpi{120} s^{m-1} تمامی ضرایب صفر شده اند، برای بدست آوردن ضرایب موجود در این سطر از آرایه راث از معادله کمکی سطر قبلی استفاده می کنیم. معادله کمکی را با مشتق گیری از روی سطری که با فلش قرمز مشخص شده است بدست می آوریم. همواره برای بدست آوردن معادله کمکی به سطر قبل از سطر تمام صفر مراجعه می کنیم. معادله کمکی را ابتدا به صورت زیر بدست می آوریم:

\dpi{120} as^{m} + bs^{m-2} + cs^{m-4} + ....

حال که معادله مشخصه را تشکیل دادیم، یک بار از آن مشتق گرفته و ضرایب حاصله را به جای صفر ها قرار می دهیم.

\dpi{120} mas^{m-1} + (m-2)bs^{m-3} + (m-4)cs^{m-5} + ...

جدول راث به صورت زیر بازنویسی خواهد شد :

اگر باز هم در جدول آرایه راث، سطر تمام صفر داشتیم باز هم الگوریتم بالا را روی آن پیاده خواهیم کرد.

نکات سطر تمام صفر در معیار پایداری راث – هورویتز :

۱ – سطری فقط می تواند به صورت کامل صفر شود که دارای اندیس فرد باشد، به عبارت بهتر فقط سطرهایی که توان S در آن ها صفر می باشد، قادر به صفر شدن هستند.

۲ – سطر تمام صفر در حالتی رخ می دهد که ریشه های متقارن نسبت به مبدا داشته باشیم. البته این نکته را باید ذکر کنیم که وجود سطر تمام صفر هیچ الزامی برای وجود ریشه موهومی روی محور jw ایجاد نمی کند. اما عکس این موضوع همواره برقرار است و اگر معادله مشخصه دارای ریشه موهومی روی محور jw باشد، حتماً  سطری از آرایه راث صفر خواهد شد.

مثال ۳ : آرایه راث متناظر با معادله مشخصه زیر را نوشته و پایداری آن را مورد بررسی قرار دهید.

\dpi{120} \Delta (s) = s^{6} + 5s^{5} + 11s^{4} + 25s^{3} + 36s^{2} + 30s + 36 = 0

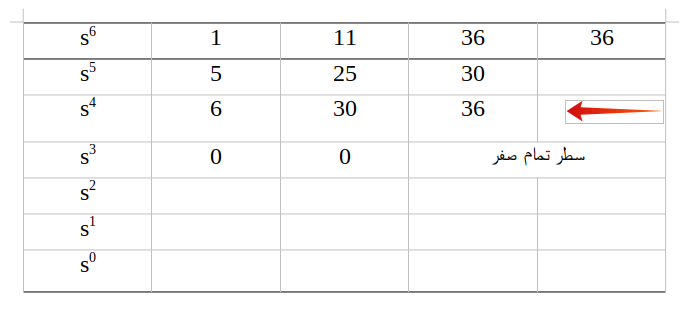
سطر تمام صفر در آرایه راث هورویتز

در جدول راث بالا مشاهده می شود که سطر \dpi{120} s^{3} صفر شده است، پس باید به وسیله سطر قبل از آن یعنی \dpi{120} s^{4} معادله کمکی را بدست می آوریم، سپس از آن مشتق گرفته و ضرایب سطر صفر را بدست آوریم.

\dpi{120} 6s^{4} + 30s^{2} + 36 = 0 \Rightarrow (s^{4} + 5s^{2} + 6)^{'} = 0 \Rightarrow 4s^{3} + 10s = 0

بعد از بدست آوردن ضرایب آن ها را در جدول راث جایگزین می کنیم و جدول راث نهایی برای این معادله مشخصه به صورت زیر خواهد بود:

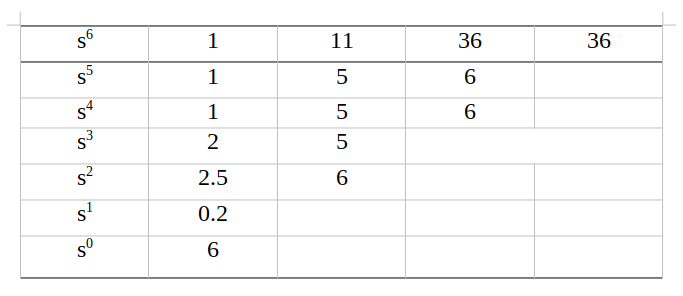
روش تشکیل آرایه راث

همانطور که مشاهده می شود در ستون اول جدول راث هیچ گونه تغییر علامتی مشاهده نمی شود، پس این سیستم هیچ گونه ریشه ای در سمت راست محور jw ندارد. اما به دلیل وجود سطر صفر این سیستم دارای چهار ریشه روی محور jw می باشد که اگر مکرر نباشند، می توان گفت که این سیستم به صورت مرزی پایدار خواهد بود. ریشه هایی از این معادله مشخصه که روی محور jw قرار دارند را می توان به وسیله حل معادله کمکی به صورت زیر بدست آورد.

\dpi{120} s^{4} + 5s^{2} + 6 = 0 \Rightarrow (s^{2} + 2)(s^{2}+3) = 0 \Rightarrow s = \pm j\sqrt{2} ; s = \pm j\sqrt{3}

مشاهده می شود که این سیستم دارای چهار ریشه موهومی روی محور jw می باشد که مکرر نیستند، پس این سیستم پایدار مرزی می باشد. چرا می گوییم پایدار مرزی ؟ به این دلیل که اگر ورودی به این سیستم اعمال شود که دارای ریشه های برابر با ریشه های این معادله باشد، در نتیجه این سیستم دارای ریشه های مکرر می گردد که به معنی بی کران شدن پاسخ این سیستم به آن ورودی خواهد بود و در نهایت سیستم ناپایدار خواهد شد.

وجود صفر در ستون اول از سطر آرایه راث 

در این حالت به خاطر وجود صفر در اولین درایه سطری از آرایه راث، عناصر در سطر بعدی بی نهایت خواهند شد و نمی توان آرایه راث را تکمیل کرد. برای این که این مشکل را حل کنیم می توانیم از سه روش استفاده کنیم که در ادامه همه آن ها را توضیح خواهیم داد.

۱ – اولین روش برای حل این مشکل استفاده از عدد مثبت بسیار کوچک به نام  می باشد، در این حالت باید به جای جمله ای که صفر شده است \dpi{120} \varepsilon قرار می دهیم و بقیه جدول راث را تکمیل می کنیم. بعد از اینکه \dpi{120} \varepsilon را جایگزین کرده و جدول را کامل کردیم مقدار \dpi{120} \varepsilon \rightarrow 0^{+} میل داده و علامت های موجود در ستون اول جدول راث را بررسی می کنیم.

۲ – می توان با جایگزین کردن \dpi{120} \frac{1}{s} به جای s معادله دیفرانسیل جدید را تشکیل داد. آرایه راث را برای معادله مشخصه اصلاح شده یعنی \dpi{120} \Delta (\frac{1}{s}) تشکیل می دهیم و مانند حالت های قبلی با آن برخورد می کنیم. تعداد ریشه ها با قسمت حقیقی مثبت برای هر دو معادله مشخصه یکسان می باشد.

۳ – در این حالت با ضرب کردن عبارت (s+a) در معادله مشخصه اصلی \dpi{120} \Delta (s) یک معادله مشخصه یک معادله مشخصه افزوده به دست می آید که به صورت زیر می باشد :

\dpi{120} \Delta _{a}(s) = (s+a)\Delta (s)

در معادله مشخصه افزوده بالا همواره a > 0 و معمولاً a = 1 قرار می گیرد. چون که (s+a) پایدار است بنابراین تعداد ریشه های ناپایدار \dpi{120} \Delta (s) و \dpi{120} \Delta _{a}(s) با هم برابر خواهند بود. پس برای بررسی پایداری سیستم جدول راث متناظر با معادله مشخصه \dpi{120} \Delta _{a}(s)  تشکیل می دهیم و مانند حالت عادی با آن برخورد می کنیم.

نکته : در روش \dpi{120} \varepsilon وقتی که \dpi{120} \varepsilon \rightarrow 0^{+} میل می کند اغلب تغییر علامت وجود دارد و سیستم ناپایدار است و حتی اگر تغییر علامت نداشته باشیم به علت رخ دادن حالت  باز هم سیستم پایداری مرزی است که برای ورودی هایی خاص ناپایدار خواهد بود و ریشه هایی روی محور موهومی خواهد داشت. 

مثال ۴ : پایداری ریشه های معادله مشخصه زیر را بررسی کنید.

\dpi{120} \Delta (s) = s^{5} + 3s^{4} + 2s^{3} + 6s^{2} + 3s + 3 = 0

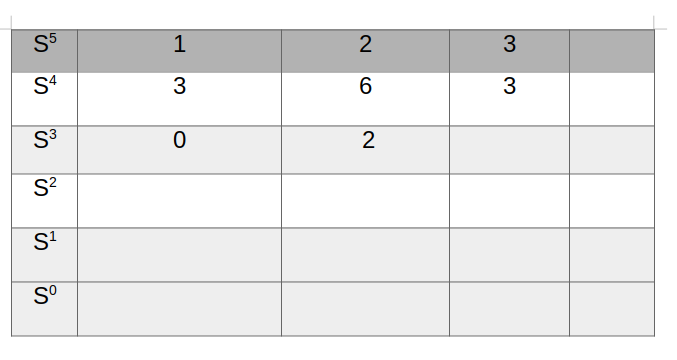
عنصر صفر در آرایه راث هورویتز

مشاهده می شود که در تشکیل جدول معیار پایداری راث – هورویتز در این مثال اولین عنصر از سطر \dpi{120} s^{3} صفر شده است پس به جای آن \dpi{120} \varepsilon قرار داده و جدول راث را به صورت زیر تکمیل می کنیم.

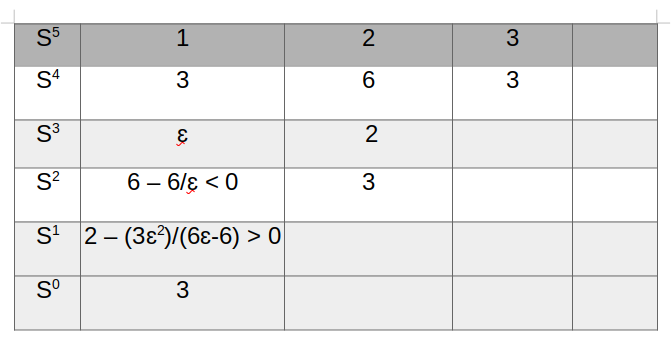
حالت های خاص در آرایه راث

مشاهده می شود به ازای \dpi{120} \varepsilon \rightarrow 0^{+} دو تغییر علامت داریم که به معنای وجود دو ریشه ناپایدار در این معادله مشخصه می باشد. 

مثال ۵ : پایداری سیستم زیر را به روش آرایه راث بررسی کنید.

\dpi{120} \Delta (s) = s^{5} + 3s^{4} + 2s^{3} + 6s^{2} + 3s + 3 = 0

این معادله مشخصه همانطور که در مثال قبل مشاهده کردیم اولین عنصر از سطر \dpi{120} s^{3} صفر خواهد شد، پس ما این مثال را به روش \dpi{120} \frac{1}{s} حل خواهیم کرد. ابتدا در معادله مشخصه به جای S  در معادله مشخصه مقدار \dpi{120} \frac{1}{s} را قرار می دهیم، پس معادله مشخصه به صورت زیر خواهد بود:

\Delta (\frac{1}{s}) = 3s^{5} + 3s^{4} + 6s^{3} + 2s^{2} + 3s + 1 = 0

حال جدول راث متناظر با این معادله مشخصه را تشکیل داده و به روش عادی به بررسی پایداری آن خواهیم پرداخت.

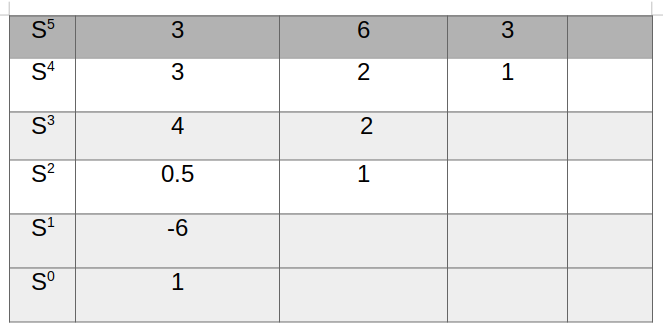
معیار پایداری راث

همانطور که مشاهده می کنید، در این حالت دیگر با عنصر صفر در سطر \dpi{120} s^{3} مواجه نشدیم. چون که در ستون اول جدول راث این سیستم دو تغییر علامت وجود دارد،‌ پس این سیستم دارای دو ریشه ناپایدار می باشد. تغییر علامت ها را در زیر مشاهده می کنید.

\dpi{120} 0.5 \rightarrow -6 \rightarrow 1

مثال ۶ : حال پایداری مثال قبل را به روش ضرب معادله مشخصه در عامل (s+a) بررسی کنید. 

در این جا ما معادله مشخصه را در عامل (s+۱) ضرب می کنیم و معادله مشخصه افزوده به صورت زیر به دست خواهد آمد.

\dpi{120} \Delta _{a}(s) = (s+1)(s^{5}+3s^{4}+2s^{3}+6s^{2}+3s+3)=0

\dpi{120} \Delta _{a}(s) = s^{6} + 4s^{5} + 5s^{4} + 8s^{3} + 9s^{2} + 6s + 3 = 0

جدول راث متناظر با معادله مشخصه جدید به صورت زیر خواهد بود.

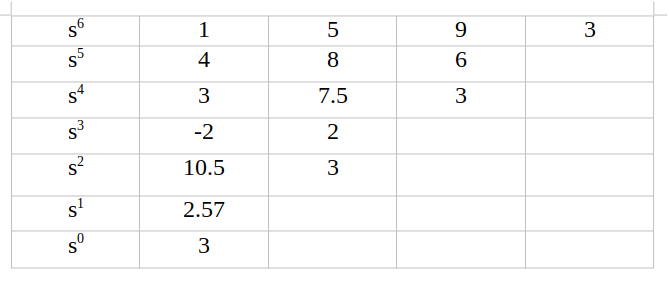
روش تشکیل جدول متناظر با آرایه راث هورویتز

همانطور که مشاهده می کنید در ستون اول این جدول دو تغییر علامت رخ داده است که به معنی وجود دو ریشه ناپایدار می باشد. این تغییر علامت ها در زیر آماده اند.

\dpi{120} 3 \rightarrow -2 \rightarrow 10.5

نکته مهم : در تمامی حالت های وقوع عنصر صفر در یک سطر از جدول آرایه راث،‌اولویت حل با روش \dpi{120} \varepsilon می باشد و اگر این روش جواب نداد به سراغ روش \dpi{120} \frac{1}{s} و (s+a) خواهیم رفت. همچنین این نکته را باید ذکر کنیم، در صورتی که روش \dpi{120} \frac{1}{s} باز هم موجب ایجاد عنصر صفر شد، دیگر این روش کارایی نخواهد داشت.

برچسب ها
یاسین بهره ملا ارسال ایمیل نوامبر 14, 2021آخرین به روز رسانی: نوامبر 15, 2021
0 3,625 خواندن این مطلب 9 دقیقه زمان میبرد
تصویر یاسین بهره ملا

یاسین بهره ملا

من یاسین بهره ملا، دانش آموخته رشته مهندسی برق این وب سایت رو تاسیس کردم تا آموخته های خودم و چیزهایی که میخونم رو اینجا به اشتراک بذارم تا شما بتونید به راحتی از اونا استفاده کنید. امیدوارم که خوشتون بیاد.

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد.

دکمه بازگشت به بالا